Se llama hipérbola al lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos, llamados focos, es una constante (se representa por 2a). La recta que une los dos focos se llama eje real de la hipérbola y la mediatriz se llama eje imaginario de la hipérbola
También podemos definirla como el lugar geométrico de los puntos P tales que la diferencia de las distancias de P a dos puntos fijos F1 y F2 es constante.
Los puntos F1 y F2 se llaman focos de la hipérbola.
Así, la hipérbola es el conjunto de puntos P que satisfacen:
| d(P,F) - d(P,l) |=2a
Elementos
- El centro (O) es el punto medio de los focos.
- El eje focal o eje mayor es la recta que pasa por los focos.
- El eje no focal o eje menor es la recta perpendicular al eje focal que pasa por el centro.
- La hipérbola es simétrica respecto a estos dos ejes, por lo que también se les llama ejes de simetría.
- Los vértices (V1 y V2) son los puntos donde la hipérbola corta al eje focal.
- La distancia entre los vértices es igual a la constante 2a que aparece en la definición de la hipérbola
Teorema
La ecuación canónica de la hipérbola con centro en
con eje transversal horizontal. Y
con eje transversal vertical
Los vértices están a una distancia de a unidades del centro y los focos a una distancia de
Procedimiento
- Cualquier punto de la hipérbola cumple:
- Esta expresión da lugar a:
Realizando las operaciones llegamos a:
Ecuacion General
Si el centro de la hipérbola es C(x0, y0) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(X0+c, y0) y F'(X0-c, y0). Y la ecuación de la hipérbola será:
Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación de la forma:
Hallar la ecuación de la hipérbola de foco F(7, 2), de vértice A (5,2) y de centro C(3, 2).
Resumen
- El centro está en
- Los vértices están en
- Los focos están en
Si el eje transversal de la hipérbola es vertical entonces - El centro está en
- Los vértices están en
- Los focos están en
Una ayuda importante para trazar la gráfica de una hipérbola son sus asíntotas. Toda hipérbola tiene dos asíntotas que se intersecan en su centro y pasan por los vértices de un rectángulo de dimensiones 2a y 2b y centro en
El segmento recto de longitud 2b que une
se llama eje conjugado de la hiperbola.
Ejemplo
Hallar la ecuación canónica, los focos, los vértices, la excentricidad y las asíntotas de la hipérbola cuya ecuación es
Completando el cuadrado en ambas variables
Por tanto, el centro está en
Los vértices están en
Los focos en
La excentricidad es
Referencias Previas
- Cónicas (circunferencia, elipse, parabola)
- Ecuasiones de primer y segundo grado
- Geometria
- Algebra
- Graficación segun el plano cartesiano































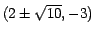



Buena investigación pero te faltó especificar las características para que la ecuación general sea una hipérbola, como por ejemplo que los coeficientes que acompañan a las variables al cuadrado deben ser de distinto signo. Por esta razón tienes un punto menos en el portafolio.
ResponderEliminar