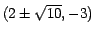Calculo I Y.Trejo

miércoles, 15 de diciembre de 2010

matematica: derivada - reglas de las derivadas

Act 4. Derivada parte II

Función trigonométrica	Derivada
y= cos(x)	y’= -sen(x)
y=sen(x)	y’= cos(x)
y=tg(x)	y’= sec $2$
y=ctg(x)	y’=-csc $2$
y=sec(x)	y’= sec(x).tg(x)
y= csc(x)	y’= -csc(x).ctg(x)

 Antes de aplicar una regla de derivación, ¿qué debes hacer, independientemente de cuál sea la función?

Analizar la función para saber que contiene y así mentalmente saber que reglas tengo que aplicar, es decir, identificar que tipo de función es

·       ¿Se puede aplicar la misma regla a todas las funciones? ¿Por qué?

No todas las funciones son iguales, por eso hay que saber que regla aplicar en cada una, puede que muchas coincidan en varias funciones pero no en todos los casos tiene que ser la misma.

·       ¿Se puede derivar una misma función utilizando reglas diferentes?. ¿Por qué?

Si, ya que hay funciones que depende de cómo se pongan se les puede aplicar reglas de derivación diferentes 

ACT 2

Antes de derivar:

¿Qué tipo de funcion es?

¿Qué tego en la funcion, es decir cada factor?

¿Qué regla es factible aplicar?

Durante la derivación:

¿Cómo se aplicaban las reglas?

Seguir cada paso luego de idetificada la funcion

Si la regla que escogimos no es la que se debia aplicar buscar otros metodos 

Despues de derivar:

Revisar el resultado

¿es logico?

Si esta errado volverlo a realizar

Act. 4 Derivadas parte I

Nombre	Enunciado (La regla de derivación expresada en palabras)	Función (Es una generalización)	Función derivada	Ejemplo
Nombre		Función (Es una generalización)	Función derivada	Función	Derivada	Planificación y argumentación
Derivada de una constante	La derivada de una constante es cero.	y = k	y’ = 0	y=ln(2)	y’ =0	Analizo la función, observo que es un número real, no depende de ninguna variable, por lo tanto su derivada es cero.
Derivada de una potencia (exponente un número real)	La derivada de una funcion exponencial,es el exponente multiplicando a la variable la cual estara elevada a el exponente menos uno.	y= xⁿ	y’ = n x^n-1	$y$ $= x 3$	$y’ = 3 x 3 - 1$ $y ’$ $= 3 x 2$	Al ver la función elevada a un exponente, tomo el exponente lo bajo para que acompañe la variable y esta la elevo al exponente menos 1.
Derivada de una constante por una función	La derivada de una constante por una función es la misma constante por la derivada de la función.	y=k f(x)	K.y’= f(x)	$y$ $= 7x$	$y’$ $= 7$	Estudio las características de la función, si es el producto de una constante por una función, derivo la función y la multiplico por la misma constante.
Derivada de una suma de funciones	La derivada de una suma (o diferencia ) de funciones es la suma (o la diferencia) de las derivadas	y=(f(x)+g(x))	y’= y’f(x) + y’g(x)	y = 3+2x⁵	y’=0+10x⁴ y’= 10x⁴	Se analiza la función, y se puede derivar cada sumando por separado.
Derivada de un producto de funciones	La derivada de una producto de funciones es la derivada de la primera función por la segunda sin derivar, más la derivada de la segunda función por la primera sin derivar	y=(f(x).g(x))	y’=y’f(x).yg(x)+f(x).y’g(x)	$h (x) = (4 x + 2)(3 x 7 + 2)$	$f (x) = (4 x + 2)$ y $g (x) = (3 x 7 + 2)$ h’(x)= $(4 x + 2)$ . $21 x 6$ +4. $(3 x 7 + 2)$ $h'(x) = 84 x 7 + 12 x 7 + 42 x 6 + 8$	Se analiza y visualiza cada uno de los productos, luego se hace la derivida del primer producto por el segundo producto sin derivar, mas el primero sin derivar por el segundo producto derivado.
Derivada de un cociente de funciones	La derivada de un cociente de funciones es un fracción que tiene por numerador la derivada del númerador por el denominador sin derivar, menos la derivada del denominador por el numerador sin derivar, todo dividido entre el denominador original al cuadrado	y= f(x)/g(x)		$y=(4 x - 2) / (x 2 + 1)$		Se analiza la funcion, luego de identificar que es un cociente, se hace la derivada del numerador por el denominador sin derivar, menos el numerador sin derivar por la derivada del denominador, todo esto entre el denominador al cuadrado.
Derivada de logaritmo neperiano	La derivada de un logaritmo neperiano es uno entre la variable del mismo. Y de un logaritmo base b, es uno por la variable de este multiplicada por el neperiano de la base	y= lnx		y= ln8 y = log₁₀(3x + 1)	y’= 1/8 y’= 1/ (3x+1)ln10	Cuando se encuentra un logaritmo neperiano, se toma la variable a la cual se le aplicara el logaritmo y se pone como denominador con numerador igual a 1 Cuando hay un logaritmo natural en base a, el conciente tendra por numerador 1 y denominador igual a la variable del logaritmo por el logaritmo neperiano de la base.
Derivada de exponencial	La derivada de una exponencial es el mismo exponencial.	y= e^x y= a^x		f(x) = e^2x g(x) = 5 ^{x – 2}	f’(x) = 2e^2x y’ = (ln 5) 5^{x – 2}	Toda funcion exponencial al derivarse su resultado es la misma funcion exponencial. Pero al derivar una exponencial de otra base, esta base quedara multiplicada por el logaritmo neperiano de ella misma.

miércoles, 3 de noviembre de 2010

Se llama hipérbola al lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos, llamados focos, es una constante (se representa por 2a). La recta que une los dos focos se llama eje real de la hipérbola y la mediatriz se llama eje imaginario de la hipérbola

También podemos definirla como el lugar geométrico de los puntos P tales que la diferencia de las distancias de P a dos puntos fijos F1 y F2 es constante.

Los puntos F1 y F2 se llaman focos de la hipérbola.

Así, la hipérbola es el conjunto de puntos P que satisfacen:

| d(P,F) - d(P,l) |=2a

Elementos

El centro (O) es el punto medio de los focos.
El eje focal o eje mayor es la recta que pasa por los focos.
El eje no focal o eje menor es la recta perpendicular al eje focal que pasa por el centro.
La hipérbola es simétrica respecto a estos dos ejes, por lo que también se les llama ejes de simetría.
Los vértices (V1 y V2) son los puntos donde la hipérbola corta al eje focal.
La distancia entre los vértices es igual a la constante 2a que aparece en la definición de la hipérbola

Teorema

La ecuación canónica de la hipérbola con centro en

con eje transversal horizontal. Y

con eje transversal vertical

Los vértices están a una distancia de a unidades del centro y los focos a una distancia de unidades del centro. Además

Procedimiento

Cualquier punto de la hipérbola cumple:

Esta expresión da lugar a:

Realizando las operaciones llegamos a:

Ecuacion General

Si el centro de la hipérbola es C(x₀, y₀) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(X₀+c, y₀) y F'(X₀-c, y₀). Y la ecuación de la hipérbola será:

Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación de la forma:

Hallar la ecuación de la hipérbola de foco F(7, 2), de vértice A (5,2) y de centro C(3, 2).

Resumen

Si el eje transversal de la hipérbola es horizontal entonces

El centro está en

Los vértices están en

Los focos están en

Si el eje transversal de la hipérbola es vertical entonces

El centro está en

Los vértices están en

Los focos están en

Una ayuda importante para trazar la gráfica de una hipérbola son sus asíntotas. Toda hipérbola tiene dos asíntotas que se intersecan en su centro y pasan por los vértices de un rectángulo de dimensiones 2a y 2b y centro en