Nature by Numbers

Act 2. Triángulo

Triángulo: es un polígono de 3 lados que se unen entre sí formando tres vértices o esquinas (de ahí su nombre de tri-ángulo) y que son además finitas desde un vértice hasta el otro, mientras que los segmentos de rectas determinados reciben el nombre de lados del triángulo.

Un triángulo cuenta con tres lados, tres vértices y tres ángulos interiores. Es habitual que se conozcan por el nombre de sus vértices, designados con letras mayúsculas. Ejm.: ABC

Clasificación según la Amplitud de sus Ángulos

• Acutángulo: sus tres ángulos interiores son agudos.
• Rectángulo: cuenta con un ángulo interior recto, formado por dos lados conocidos como catetos, mientras que el restante recibe el nombre de hipotenusa.
• Obtusángulo: uno de sus ángulos es obtuso.

Clasificación según el Tamaño de sus Lados

• Equilátero:  sus tres lados tienen la misma longitud.
• Isósceles: dos de sus lados tienen la misma longitud.
• Escaleno: todos sus lados tienen diferentes longitudes. 

Rectas y Puntos Notables

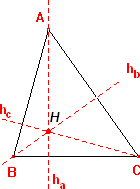
• Altura: la recta perpendicular a un lado del triángulo que pasa por el vértice opuesto.

La altura  respecto del lado 'a'=BC, se denota por h_a

La altura  respecto del lado 'b'=AC, se denota por h_b 

La altura respecto del lado 'c'=AB, se denota por h_c

 

Nota 1: Una altura puede ser interior al triángulo, exterior al mismo, o incluso, coincidir con alguno de sus lados (según el tipo de triángulo)

Si el triángulo es RECTÁNGULO:

La altura respecto a la hipotenusa es interior, y las otras dos alturas coinciden con los catetos del triángulo  

Si el triángulo es ACUTÁNGULO:

Las tres alturas son interiores al triángulo 

Si el triángulo es OBTUSÁNGULO:

La altura respecto al mayor de sus lados es interior, siendo las otras dos alturas exteriores al triángulo

Nota 2:  En un triángulo isósceles, la altura correspondiente al lado desigual divide el triángulo en dos triángulos iguales.

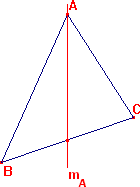
• Mediana: la recta que une el vértice correspondiente del triángulo con el punto medio del lado opuesto

Mediana correspondiente al vértice A, se denota por  m_A

Mediana correspondiente al vértice B, se denota por  m_B 

Mediana correspondiente al vértice C, se denota por  m_C

 



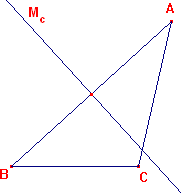
• Mediatriz: la recta perpendicular a un lado del triángulo que pasa por su punto medio

La mediatriz del lado 'a'=BC, se denota por M_a
La mediatriz del lado 'b'=AC, se denota por M_b
La mediatriz del lado 'c'=AB, se denota por M_c

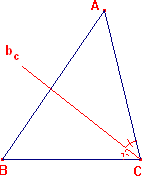
• Bisectriz: recta que pasando por uno de sus vértices, divide al ángulo correspondiente en dos partes iguales. Todo triángulo ABC tiene tres bisectrices

Bisectriz correspondiente al ángulo A, se denota por b_A
Bisectriz correspondiente al ángulo B, se denota por b_B
Bisectriz correspondiente al ángulo C, se denota por b_C

• Ortocentro: punto de intersección de las tres altitudes de un triángulo

El Ortocentro de un triángulo rectángulo es el vértice correspondiente al ángulo recto.
El Ortocentro de un triángulo acutángulo está en el interior del triángulo.
El Ortocentro de un triángulo obtusángulo está en el exterior del triángulo.

• Baricentro: es el punto de intersección de las medianas de cada uno de los lados de un triángulo

  
  

  

  
  

  El baricentro de un triángulo, es un punto interior al mismo, que dista el doble de cada vértice que del punto medio de su lado opuesto.

  • Circuncentro: punto de intersección de las tres mediatrices de cada uno de los lados de un triángulo.

  
  

  

  
  

  1. El Circuncentro de un triángulo rectángulo es el punto medio de la hipotenusa.
  2. El Circuncentro de un triángulo acutángulo está en el interior del triángulo.
  3. El Circuncentro de un triángulo obtusángulo está en el exterior del triángulo.

  
  

  • Incentro: punto de intersección de las bisectrices de cada uno de los lados de un triángulo
    
    
    
    
    
    El incentro de un triángulo cualquiera está siempre en el interior del triángulo
    
    
    ACTIVIDAD 2
    
    
    En el video mostrado se denota uno de los conceptos que se definió en esta publicación que es la mediatriz
    
    
    
    
    
    Como se muestra en la siguiente imagen que se transmite en el video, al tomar los dos puntos rojo y azul, trazamos una línea que los une y después otra perpendicular a esta justo por la mitad, encontrando así la mediatriz del segmento de unión de estos dos puntos, que se pudiera denotar como si fuera uno de los lados del triángulo.
    Al añadirle un tercer punto verde como se denota en la imagen generamos dos nuevas mediatrices que se interseccionan con la primera.
    
    
    
    
    Opinión Personal
    
    
    A primera vista no entendí la esencia del video, me pareció llamativo ya que formas geométricas se relacionaban con la naturaleza como lo es la libélula y los polígonos de sus alas, más a través de leer el apartado que explicaba cada uno de los conceptos y teorías que el video explicaba fue más fácil entenderlo y me quede impresionada de lo sabía que puede ser la naturaleza y que en simples detallas que podemos encontrar hay matemática inculcada.
    
    
    
    http://www.etereaestudios.com/docs_html/nbyn_htm/about_index.htm
    
    
    
    

Act 1. El Cálculo

El Cálculo: es la matemática del movimiento y el cambio. Donde haya movimiento o crecimiento, donde fuerzas variables produzcan aceleración, el cálculo es la rama de las matemáticas que debemos aplicar.

Experiencia

Un experiencia de la vida cotidiana donde utilizo cálculo puede ser:

·         Al tener que ir de viaje se hace una selección del tamaño de la maleta para guardar toda la ropa con respecto al número de días que se va, es decir que se hace el cálculo de el tamaño en relación con el número de días que se estará de viaje.  Mientras más tiempo más ropa, más grande es la maleta pero si se va por un plazo corto de días la maleta disminuiría su tamaño.

·         En la apertura de las llaves de la ducha al bañarnos para medir la presión con la que la queremos y  para que el agua salga más fría o caliente, es decir, al bañarnos  hacemos el cálculo de primero la presión con que queremos que salga el agua si queremos mucha se abren más las llaves sino se abre un término medio, además de la temperatura ya que no queremos ni congelarnos con agua muy fría ni quemarnos con agua muy caliente, por ello se hace el cálculo de un término medio en cuanto a la temperatura que utilizaremos para ducharnos.

·         Otro ejemplo a reseñar, es la fuerza con la que hay que pegarle al balón de Voleibol para pasar la malla y que este no se pase de la raya en la cancha contraria ni quede de nuestro lado.

Cálculo en Ingeniería Civil

Una Aplicación del cálculo en Ingeniería Civil pudiera ser para el dimensionamiento del volumen de un tanque de almacenamiento de agua potable para abastecer a una población determinada